|
Every hollow body with an opening to the outside is a Helmholtz-Resonator
|
So is a guitar, a violin even a drum, or any other musical instrument that fulfills the marks:
- hollow body
- opening to the outside
... regardless of the shape of the instrument and the shape of the so-called 'soundhole'.
The background and basics
The effect of 'Helmholtz resonance' was revealed by Hermann von Helmholtz in the late 1850s.
An indispensable mark of such a Helmholtz resonator is its 'Helmholtz resonator frequency'. This is the frequency where one gets a tremendous over-shot in sound strength at the opening (e.g. a 'soundhole') compared to the emitted strength of sound of the body if the body is stimulated by a mechanical frequency. (See Wikipedia for "Helmholtz Resonance" and/or "Helmholtz Resonator")
An excellent article about Helmholtz resonance [↑] can be found at the University of New South Wales (UNSW) in Sydney/Australia and the 'Basics' section [↑] provides essential knowledge about the physics of musical instruments and the human voice as well.
Bringing this into practice ...
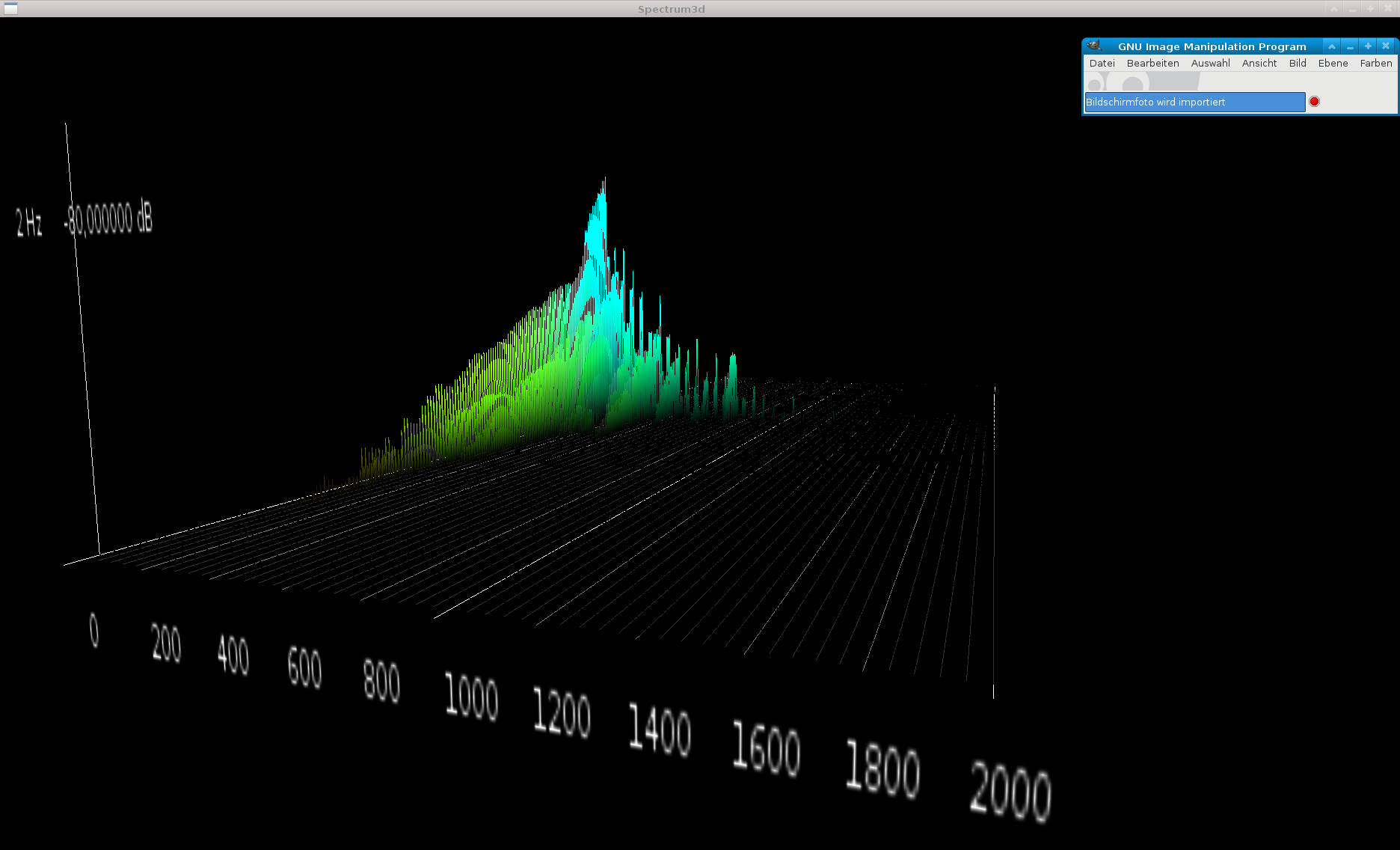
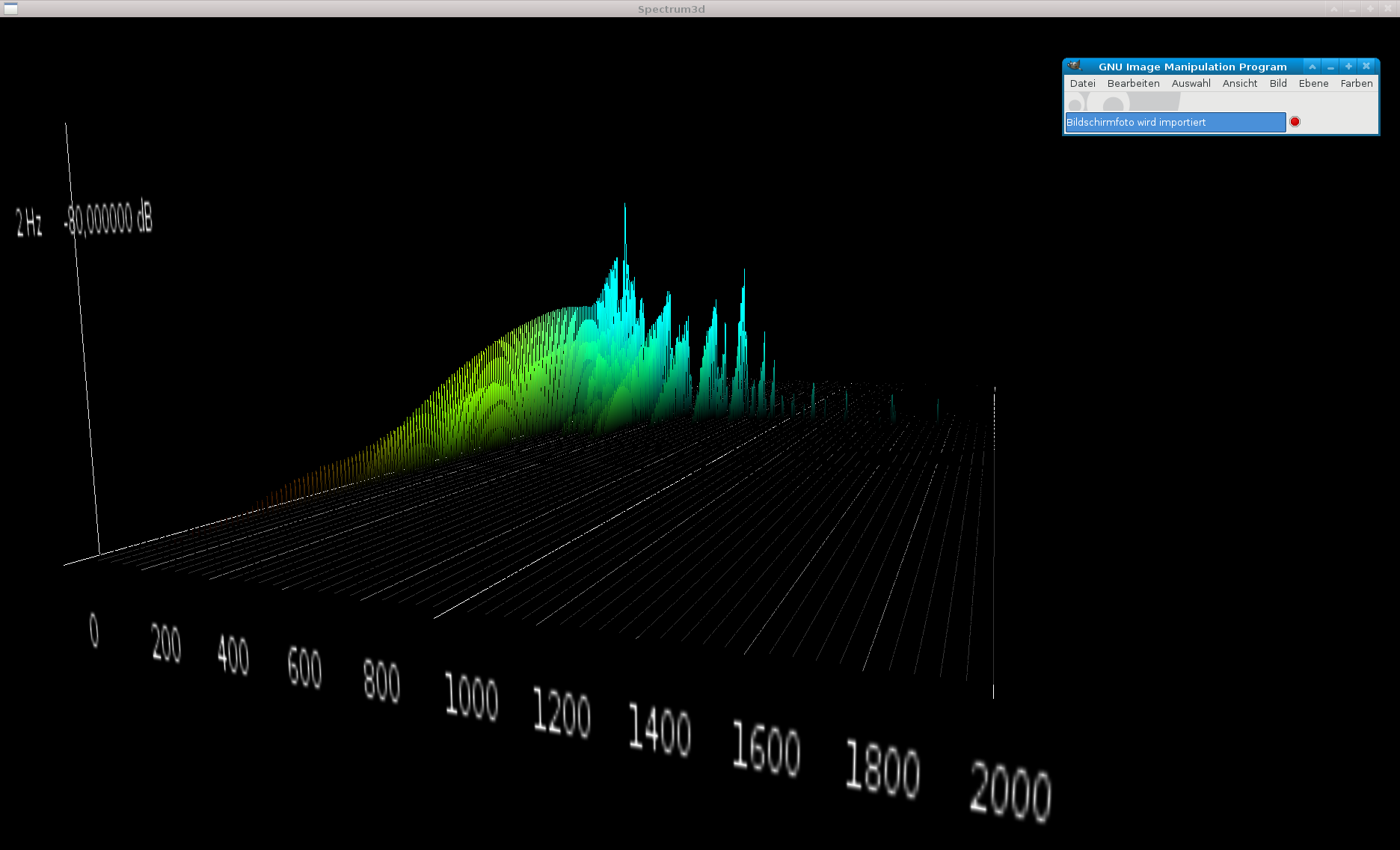
Below are two pictures from a 3D-spectrum analyzer.
These pictures show the impact of the Helmholtz-Resonator-Frequency on an instrument if the soundhole is not covered and if the soundhole is covered. I.e. the opening is closed and therefore the Helmholtz-Resonator is 'turned off. Mounted into the instrument was an AnyMic/i from normal production.
The chosen instrument was a Western-/Steel-string guitar with a typical Helmholtz-Resonator-Frequency of 55 Hertz. This is half of the frequency of the base-frequency that is for a steel-string guitar the open A string (A5; 110 Hz). The bad impacts of an uncovered soundhole can be seen clearly ...
 |
 |
|
UN-covered soundhole
|
Covered soundhole
|
Using an internal microphone in the instrument demands, that the soundhole is covered by a 'soundhole cover'.
Only this turns the Helmholtz-Resonator 'off'' with all the bad impact. Some call that a 'feedback killer' - which is wrong because Helmholtz-Resonance has nothing to do with 'feedback'.
Specific instruments have typical H.R. frequencies.
I can speak here only for instruments, for which I have investigated or tested with the instrument I have at hand.
The following table shows the results of my investigations and measures:
| H.R. frequency [Hz] | Base frequency [Hz] | Note/Tone | |
| Steel-string guitar | 55 | 110 | A5 (open A string) |
| Classical guitar | 48 | 96 | G5 |
| Flamenco guitar | 43 | 86 | F#5 |

